According to Encyclopedia.com, “linear algebra originated as the study of linear equations.” Linear algebra deals with vectors, matrices and vector spaces. Before the 1950s, it was part of Abstract Algebra (Tucker 1993). For example, the book “A Survey of Modern Algebra” by Garrett Birkhoff and Saunders Mac Lane (3rd edition, Macmillan Company, New York, 1965) contains three chapters of linear algebra materials out of its 15 chapters: Chapter 7 (Vectors and Vector Spaces), Chapter 8 (The Algebra of Matrices), and Chapter 10 (Determinants and Canonical Forms).
In 1965 the Committee on the Undergraduate Program in Mathematics, Mathematical Association of America (MAA), outlined the following topics for a stand alone linear algebra course: Linear systems, matrices, vectors, linear transformations, unitary geometry with characteristic values.
The first stand-alone book that was named “Linear Algebra” in the United States might be that by Charles W. Curtis of the University of Wisconsin-Madison, published in 1963 by Allyn and Bacon, Inc., Boston. The book title is “Linear Algebra: An Introductory Approach.” This book contains all the materials defined by MAA in 1965. Most linear algebra books today would also cover these materials, plus some modern materials on singular value decomposition (SVD) (Strang 2016). Modern advanced materials may include spectral theorem, Jordan forms, polynomials, and Cayley-Hamilton theorem (Garcia and Horn 2022).
Paul R. Halmos’ book “Finite-Dimensional Vector Space” was mostly about linear algebra although did not name so. This book was first published in 1942 and had its second edition in 1958. However, the book missed an important part of linear algebra: The solution of a set of linear equations, which became extremely important in the 1960s when computer applications for solving many linear equations in engineering were popular due to the invention of the finite element method.
Although Jean Dieudonne’s book “Linear Algebra and Geometry” in 1964 bore the name of Linear Algebra, focused mainly on linear transforms, and had no solutions of linear equations either. Ross A. Beaumont’s 1965 book also had its name“Linear Algebra”, but again contained no materials on linear equations.
Modern linear algebra books have more materials on rectangular matrices, SVD, data science applications, graphic visualization, and computer codes. Our book is in this category in terms of materials. In the methodology aspect of learning and teaching, we use progressive education pedagogy and emphasize intuition, graphics, storytelling, computing, and rigorous proof.
Every chapter starts with elementary materials and common sense, and can be understood without reading previous chapters. Almost all the chapters include advanced materials which are prepared for the second-semester linear algebra course, or called advanced linear algebra. These advanced materials can be used as a research handbook or as advanced examples to support a research project. Different from the traditional linear algebra book, chapters are entitled according to the nature of the relevant theory, e.g., linear transform and vector space, our chapters are entitled according to the usage or functions of a method, e.g., Data matrices, operations, and visualizations for Chapter 1, and Space-time decomposition: SVD for Chapter 2. We follow the RUM principle when selecting materials. Here R is for Relevant to both courses and research in the science; U is for Useful to not only the courses and research, but also to future jobs; and M is for Modern, incorporating recent progress and tools, especially progress in computing and data science. In this book, our modern materials are reflected in SVD applications, matrix visualization, machine learning, and the use ChatGPT, Python, and R.
Meeting these RUM criteria in courses, including linear algebra, will require time and commitment to changing the curricula of relevant study programs to better support students learning. Progress will be incremental. Mathematics courses and instructors can both evolve to help meet the objective of well-educated students prepared for successful careers.
In terms of the book style, we follow the principle of interaction. We make sure that each method has a computer code to allow a reader to interact with the book. Traditional linear algebra books, like most other math books, often stack with definitions of mathematical objects, such as subspace, and isomorphism, dense formulas, and awkwardly-worded theorems. The theorem statements are only comprehensible by professional mathematicians in the name of “mathematical rigor,” with which mathematicians are extremely proud of.
Bearing in mind that most students of linear algebra are not going to become professional mathematicians, this book tries to do it differently. We start with common sense, data, visualization, examples, and interpretations that lead to names, definitions, and theorems. Most math objects in our book are named after the objects have appeared in a computational process or an algorithm, so that students have an image in their mind before we name them. This is like that the 10-year-old Mike learns to name Uncle Tom after seeing him, in contrast to the legendary Uncle Tom who suddenly appears in front of Mike.
Despite our emphasis on the details of modern and useful materials, the book still includes almost all the contents of a conventional linear algebra book, such as vector spaces, inner product space, linear equations, orthogonality, eigenvectors, SVD, linear transform, polynomials, operators, spectral theory, Jordan forms, Cayley-Hamilton theorem, and determinants. Of course, some materials are very brief, such as determinants.
Another feature of this book is to minimize the use of mathematical symbols and notations. We understand that professional mathematicians do not mind fancy notations, but non-mathematicians may be scared away by them. Instead, we use some repeated notations for matrices. When we introduce a name and a notation, we attempt to justify its use from the perspectives of history, interpretation, and applications. This way may help a reader to develop a picture in her mind when reading a method, or a definition. We use visualization as much as we can, such as the visualization of a data matrix, and that of left and right eigenvectors from SVD.
We follow the education theory of learning-by-doing, which in our case means using your computer and our R or Python code to interact with our book and modifying our computer codes and websites to analyze your own data and generate corresponding figures. Learning-by-doing is the core methodology of the progressive education of John Dewey (1859-1952), an American philosopher and educator. Dewey felt that the experience of students and teachers together yields extra value for both. Instructors are not just to lecture and project authority, instead they are to collaborate with students and guide to students to gain experience of solving problems of their interest. Although Dewey’s education theory was established initially for school children, we feel that the same is applicable to undergraduate and graduate students. Our way of learning-by-doing is to enable students to use R or Python code and other resources in the book and its website to reproduce the figures and numerical results in the book. Further, students can modify the computer code and solve their own problems, such as visualizing the health data or weather data in a similar format and of their own interest, or analyzing their own data using a similar or a modified method. Thus, the audience interaction with the book is the main innovative feature of our book, which allows the audience to gain experience of practicing, thinking, applying, and consequently understanding. The ancient Chinese educator Confucius (551-479 BC) said that “I hear, and I forget; I see, and I remember; and I do, and I understand.” Although John Dewey and Confucius were approximately 2,500 years apart, they shared a similar philosophy of learning-by-doing.
As illustrated in Fig. 0.1, our pedagogy has three stages: Do, reflect, and apply. The author has systematically practiced this pedagogy since 2015 when he created and taught the course Climate Mathematics at the Scripps Institution of Oceanography. Usually, he presents a question or a problem at the beginning of a class. Then he asks students to orally ask the same question, or describe the same problem, or answer his question in their own words. For example, why the tiny amount of carbon dioxide in the atmosphere is important for climate change? Next, he and students search and re-search for data and literature, work on the observed carbon dioxide data at Mauna Loa using computer data visualization to see the 30% increase of carbon dioxide in the atmosphere since 1958, and discuss the structure of greenhouse gasses whose molecules have three or more atoms. Next, he encourages his students to share their experiences with their grandparents, other family members, or friends. Finally, students apply the skills gained to solve their own problems with their own data, by doing homework, working on projects, finding employment, or making innovations. In this cycle, students have gathered experience and skills to improve their life and to engage with the community. In the short term, students trained in this progressive cycle of learning-by-doing have a better chance to become a good problem solver, a smooth story narrator, and an active leader in a research project in a lab or an internship company, and consequently become competitive in the job market. In the long term, the students trained in this cycle are likely to become to a life-time learner and educator. John Dewey said that “Education is not preparation for life but life itself.” We would like to modify this to that “Education is not only preparation for a better life, but also is life itself.”
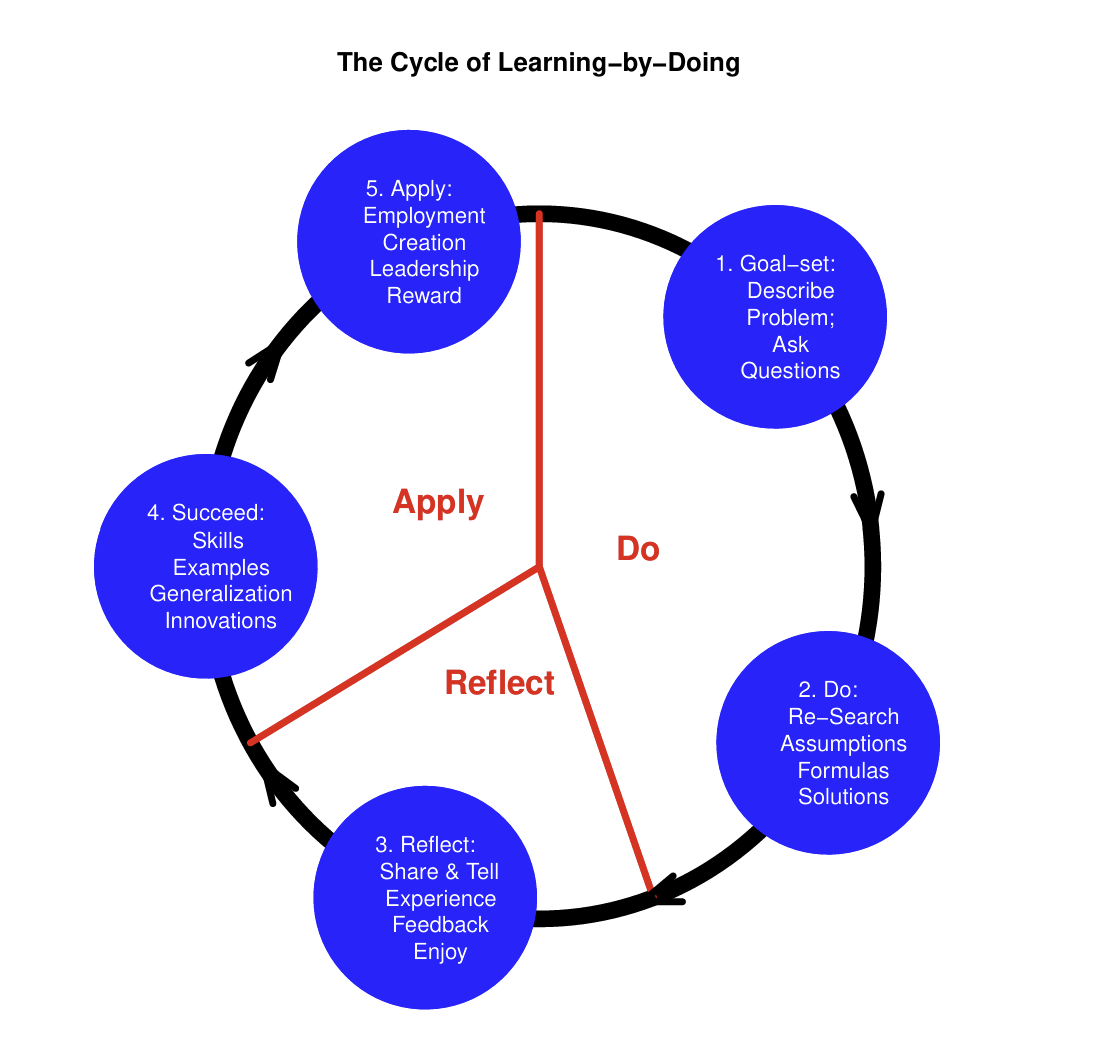
Dewey’s progressive education theory is in a sharp contrast to the traditional learning process based on the logic method, which aims at cultivating highly achieved scholars. The commonly used pedagogy of lecture-read-homework-exam often uses the logic-based approach. The climax of the logic-based education is that the instructor has the pleasure to enjoy presenting her method and theory, while students are so creative that they will produce a new or a better theory. Many outstanding scholars went through their education this way, and many excellent textbooks were written in this approach. However, our book does not follow this approach, since our book is written for the general population of students, not just for the elite class or even scholars-to-be. If you wish to be such an ambitious scholar, then you may use our book very differently: you can read the book quickly and critically for gaining knowledge instead of skills, and skip our reader-book interaction functions.
Our pedagogy is result-oriented. Our philosophy is to minimize the mathematical challenge, but to deepen the understanding of the ideas using visual tools and using story-telling experience. Our audience will be able to make an accurate problem statement, ask pointed questions, set up linear algebra models, solve the models or establish theorems, prove the theorems in both intuitive and rigorous ways, and interpret solutions and theorems using both daily life language and rigorous mathematical language. Therefore, instead of training the few “mechanics” with a high risk of failure, we wish to train a large number of good “drivers” with a large probability of success, although this book also tries to inspire a few students to become “mechanics.”
Samuel S. P. Shen San Diego, California, August 2024
We thank the friendly editorial team of Cambridge University Press (CUP) for their professional and high quality work.
References
1. Beaumont, R. A., 1965. Linear Algebra. Harcourt, Brace & World, Inc., NewYork.
2. Birkhoff, G. and Mac Lane, S., 2017. A survey of modern algebra. 3rd edition, Macmillan Company, New York, 1965.
3. Curtis, C.W., 1963. Linear algebra: an introductory approach. Allyn and Bacon, Inc., Boston.
4. Garcia, S.R. and Horn, R.A., 2023. Matrix Mathematics: A Second Course in Linear Algebra. 2nd edition, Cambridge University Press.
5. Grothendieck, A., Dieudonn, J. and Dieudonn, J., 1964. Elments de gomtrie algbrique. Hermann, Paris.
6. Halmos, P.R., 1958. Finite-dimensional vector spaces. 2nd edition, D. Van Nostrand Company Inc., Princeton.
7. Strang, G., 2016. Introduction to linear algebra. 5th edition, Wellesley-Cambridge Press.
8. Tucker, A., 1993. The growing importance of linear algebra in undergraduate mathematics. The college mathematics journal, 24(1), pp.3-9.